Fibrewise CW-complexes and Fibrewise Morse Theory


Jean-Pierre Meyer
Johns Hopkins University

Classical homotopy theory has been well-developped both in the category of topological spaces and of G-spaces (topological spaces with a continuous action by a topological group G). In the category of interest to us, namely that of spaces over a fixed base-space B, whose objects are 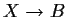$X \rightarrow B$, one can also do homotopy theory. This was first discovered 30 years ago by a number of people independantly. However, the theory is not nearly as complete as in the other two contexts. This is primarily due to the lack of a good definition of CW-complex.

Recalling how classical Morse theory, via the use of Morse functions, yields CW-complex structures on smooth manifolds, we consider fibrewise Morse functions for a submersion (or smooth fibre bundle) 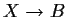$X \rightarrow B$ and study how such Morse functions yield geometric information on X. This study, together with the categorical approach to homotopy using Quillen's ``model categories", suggests a tentative definition of fibrewise CW-complexes. If a conjecture concerning these objects turns out to be true, this will be the desired correct notion of fibrewise CW-complex.