若木宏文
Date: 99.5.11, 数学教室談話会
分散共分散行列が等しい二つの多変量正規母集団、
判別ルール R の良し悪しの基準の一つは、適当な正の定数c1, c2 によ
って、r(R)
![]()
![]() と表され、r(R) が小さいほど、R は
望ましい判別ルールとされる。
と表され、r(R) が小さいほど、R は
望ましい判別ルールとされる。
![]() の値がわかっているときには、r(R)を最小にする判
別ルールは、
の値がわかっているときには、r(R)を最小にする判
別ルールは、
![]() によって与えられる。
によって与えられる。
未知母数
![]() の値が未知の場合の判別ルールとして代表的な
ものに(標本)線形判別ルールと最大尤度比ルールがある。
線形判別ルールは、Wルールとも呼ばれ、未知母数
の値が未知の場合の判別ルールとして代表的な
ものに(標本)線形判別ルールと最大尤度比ルールがある。
線形判別ルールは、Wルールとも呼ばれ、未知母数
![]() の値
を、それぞれの不偏推定量、
の値
を、それぞれの不偏推定量、
![]() で置き換えたものである。ここで、
で置き換えたものである。ここで、
![]() である。
最大尤度比ルールはZルールとも呼ばれ、判別問題を2つの仮説
である。
最大尤度比ルールはZルールとも呼ばれ、判別問題を2つの仮説
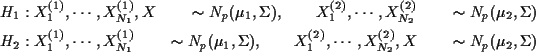
の仮説検定と考えることによって得られる。Zルールは
![]() と表される。ここで、
d(x,y;Z) = (x-y)'Z-1(x-y), c はr(RZ)が小さくなるように
c1, c2 の比に応じて決められる。
と表される。ここで、
d(x,y;Z) = (x-y)'Z-1(x-y), c はr(RZ)が小さくなるように
c1, c2 の比に応じて決められる。
線形判別ルールと最大尤度比ルールの優劣を調べるため、
![]() のときの各ルールの
r(R) の漸近展開を求める。線形判別ルールは、
のときの各ルールの
r(R) の漸近展開を求める。線形判別ルールは、
![]() と表されるので、単に2つの判別ルールの優劣を
調べるだけでなく、RW, RZを含む判別ルールのクラス,
と表されるので、単に2つの判別ルールの優劣を
調べるだけでなく、RW, RZを含む判別ルールのクラス,
![]() を考え、r(R(a,b))の漸近展開のO(n-2)までの項を最小にするよ
うな係数a, bの値を求めることを考えた。
を考え、r(R(a,b))の漸近展開のO(n-2)までの項を最小にするよ
うな係数a, bの値を求めることを考えた。
r(R(a,b))はa,bだけでなく、
![]() のマハラノビス距離
のマハラノビス距離
![]() の値にも依存しており、
の値にも依存しており、
![]() に関して一様にr(R(a,b))を最小にすることが望まれる。残念なが
ら、一様に最小にするa,bは存在しないが、任意にb を
固定したとき、
に関して一様にr(R(a,b))を最小にすることが望まれる。残念なが
ら、一様に最小にするa,bは存在しないが、任意にb を
固定したとき、![]() に関して一様にr(R(a,b))を最小にするa を求める
ことができた。c1 = c2 の場合には最適なaは、
最大尤度比ルールに対応するものとO(n-1)まで一致しており、漸近展開に
おける2次のオーダーまででは、最大尤度比ルールは、
線形判別ルールより優れていることが示された。
に関して一様にr(R(a,b))を最小にするa を求める
ことができた。c1 = c2 の場合には最適なaは、
最大尤度比ルールに対応するものとO(n-1)まで一致しており、漸近展開に
おける2次のオーダーまででは、最大尤度比ルールは、
線形判別ルールより優れていることが示された。