Some results for nonlinear equations and systems of ode's
with p-laplacian like operators.

Raul Manásevich

Centro de Modelamiento Matemático and Departamento de Ingeniería Matemática, F.C.F.M., Universidad de Chile,
Casilla 170, Correo 3, Santiago, Chile
E-mail: manasevi@dim.uchile.cl

Let us consider the so-called one-dimensional p-Laplacian operator $(\phi_p(u'))',$ where p > 1 and $\phi_p:{\mathbb R}\to{\mathbb R}$ is given by $\phi_p(s)=\vert s\vert^{p-2}s$ for $s \neq 0$ and $\phi_p(0) = 0.$ Problems with separated two-point boundary value or periodic conditions containing this operator have received a lot of attention lately with respect to existence and multiplicity of solutions.

Our aim in this talk is to deal with existence of periodic solutions to some system cases involving fairly general vector-valued operator $\phi.$Thus we will consider the boundary value problem

 

$$(\phi(u'))'=f(t,u,u'), \quad u(0)=u(T), \; u'(0)=u'(T),$$ (1)

where the function $\phi:{\mathbb R}^N\to {\mathbb R}^N$ satisfies some monotonicity conditions which ensure that $\phi$ is an homeomorphism onto ${\mathbb R}^N.$As a consequence our results will apply to a large class of nonlinear operators $(\phi(u'))',$ which for example contain some vector versions of p-Laplacian operators like the case when for $x=(x_1,\cdots,x_N)\in{\mathbb R}^N,$ $\phi(x)=\psi_p(x)\equiv \vert x\vert^{p-2}x,$ for $x \neq 0,$ $\psi_p(0) = 0,\;(p>1),$and the case when $\phi(x)= \Bigl(\phi_{p_1}(x_1),\cdots \phi_{p_N}(x_N)\Bigr),$ 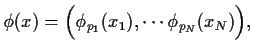with, for each $i=1,\cdots,N,$ p_i>1, and $\phi_{p_i}:{\mathbb R}\to {\mathbb R}$ is a one dimensional p_i-Laplacian.