Raul Manásevich
Centro de Modelamiento Matemático and
Departamento de Ingeniería Matemática, F.C.F.M.,
Universidad de Chile,
Casilla 170, Correo 3, Santiago, Chile
E-mail: manasevi@dim.uchile.cl
Let us consider the so-called one-dimensional p-Laplacian operator
![]() where p > 1 and
where p > 1 and
![]() is given by
is given by
![]() for
for ![]() and
and
![]() Problems with separated two-point boundary value or periodic conditions
containing this operator have received a lot of attention lately with
respect
to existence and multiplicity of solutions.
Problems with separated two-point boundary value or periodic conditions
containing this operator have received a lot of attention lately with
respect
to existence and multiplicity of solutions.
Our aim in this talk is to deal with existence of periodic solutions to
some system cases involving fairly general vector-valued operator
![]() Thus we will consider the boundary value problem
Thus we will consider the boundary value problem
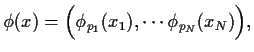 with, for each
with, for each