next up previous
Next: 参考文献

非線形 Schrodinger 型方程式の作用素論的扱い



岡沢     登（東京理科大学・理学部）




The purpose of this talk is to present a new existence theorem for the nonlinear Schrodinger equation. The theorem is an answer to the open conjecture.

Let $\Omega$ be a bounded or unbounded domain in $\mathbb R^N$ with compact C2-boundary $\partial\Omega$. In $L^2(\Omega):=L^2(\Omega; {\Bbb C})$ we consider the nonlinear Schrodinger equation

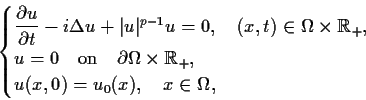\begin{displaymath}\begin{cases} \dfrac{\partial u}{\partial t}-i\Delta u+\vert... ... u(x,0)=u_{0}(x), \quad x \in \Omega,& \end{cases}\tag{NLS} \end{displaymath} (NLS)

where $i = \sqrt{-1}$, the exponent $p \ge 1$ is a constant and u is a complex-valued unknown function. It is known that (NLS) admits a unique global strong solution under the following condition:


The following conjecture remains open.


Conjecture (Pecher and von Wahl [2], 1979). p0:=(N+2)/(N-2) is the largest possible exponent for the global existence of strong solutions to (NLS).


However, we can prove the global existence for all exponents $p \ge 1$beyond their conjecture.


Theorem ([1]). Let $p \ge 1$. Then for any $u_{0} \in H^2(\Omega) \cap H^1_0(\Omega) \cap L^{2p}(\Omega)$ there exists a unique global strong solution u(t):=u(x,t) to (NLS) in $L^2(\Omega)$ such that
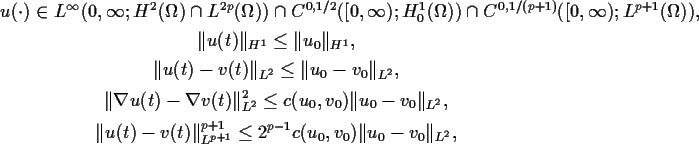
\begin{gather*}u(\cdot) \in L^{\infty}(0, \infty;H^2(\Omega) \cap L^{2p}(\Omega)... ...L^{p+1}}^{p+1} \le 2^{p-1}c(u_0,v_0) \Vert u_0 - v_0 \Vert _{L^2}, \end{gather*}
where v(t) is a solution to (NLS) with initial value $v_0 \in H^2(\Omega) \cap H^1_0(\Omega) \cap L^{2p}(\Omega)$.



 
next up previous
Next: 参考文献
Tohru Okuzono 平成12年6月5日