


Next: About this document ...
Integral geometry by sheaves and 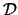 -modules
-modules
Corrado Marastoni
Hiroshima, January 8 2002
In this talk we shall try to convince the audience, by using a
motivational introduction through the Radon and the Penrose
transforms, that the approach by sheaves and 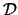 -modules is
well-suited for the study of integral geometry.
Here is a brief sketch of our program.
-modules is
well-suited for the study of integral geometry.
Here is a brief sketch of our program.
- (1)
- What are the Radon and the Penrose transforms?
What is behind the fact that their ranges are
characterized essentially by the same system of linear
PDEs?
- (2)
- Brief introduction to sheaves (used to describe the
geometry and
regularity --analytic,
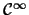 , ...-- of the
desired solutions) and
, ...-- of the
desired solutions) and 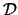 -modules (to describe
the systems of linear PDEs appearing in the problem).
-modules (to describe
the systems of linear PDEs appearing in the problem).
- (3)
- Adjunction formulas : i.e., how do sheaves and
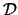 -modules fit together in order to describe the
transform?
-modules fit together in order to describe the
transform?
- (4)
- Group invariance : when one deals with compact
homogeneous manifolds of some complex semisimple Lie group
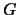 (as are, for example, the projective space or, more
generally, the Grassmannians for
(as are, for example, the projective space or, more
generally, the Grassmannians for
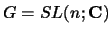 ), and
the problem is
), and
the problem is 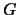 -invariant, things become clearer.
-invariant, things become clearer.
- (5)
- The concrete case of complex Radon-Penrose transform :
the answer to the second question of (1) is that the Radon
and the Penrose transforms are induced --as well as various
other classical real or complex problems-- by the
same overlying complex integral transform.
In performing the above program, we shall use the results
obtained in our recent joint works with T. Tanisaki (to
appear in ``Differential geometry and its Applications'')
for the 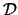 -module side of the problem, and with A. D'Agnolo (Publications R.I.M.S. Kyoto, vol. 36, 2000,
p. 337-383) for the sheaf-theoretic part.
-module side of the problem, and with A. D'Agnolo (Publications R.I.M.S. Kyoto, vol. 36, 2000,
p. 337-383) for the sheaf-theoretic part.



Next: About this document ...
Tohru Okuzono
2001-12-20
![]()
![]() -modules is
well-suited for the study of integral geometry.
Here is a brief sketch of our program.
-modules is
well-suited for the study of integral geometry.
Here is a brief sketch of our program.
![]() -module side of the problem, and with A. D'Agnolo (Publications R.I.M.S. Kyoto, vol. 36, 2000,
p. 337-383) for the sheaf-theoretic part.
-module side of the problem, and with A. D'Agnolo (Publications R.I.M.S. Kyoto, vol. 36, 2000,
p. 337-383) for the sheaf-theoretic part.