


Next: About this document ...
Estimation of the noncentrality matrix of a noncentral Wishart
distribution with unit scale matrix, employing a matrix loss
function
Heinz Neudecker (University of Amsterdam)
Consider
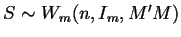 . The habitual unbiased estimator of
. The habitual unbiased estimator of
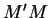 is
is 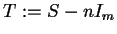 . Under certain conditions
. Under certain conditions
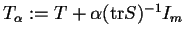 is better than
is better than 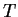 , for suitable
, for suitable
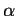 . Leung (1994) showed this using the loss function
. Leung (1994) showed this using the loss function
We shall use a matrix loss function
and apply Lywner partial ordering of symmetric matrices.
An approximate domination result will be proved, the error term being
of order 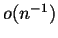 . We shall use a matrix version of a Fundamental
Identity
for the noncentral Wishart distribution. [Leung gave a scalar version
extending Hass's Fundamental Identity (scalar version) for the central
Wishart distribution.] A matrix version of Leung's ancillary Lemma 3.1 will
then be established. We shall employ an approximation of
. We shall use a matrix version of a Fundamental
Identity
for the noncentral Wishart distribution. [Leung gave a scalar version
extending Hass's Fundamental Identity (scalar version) for the central
Wishart distribution.] A matrix version of Leung's ancillary Lemma 3.1 will
then be established. We shall employ an approximation of
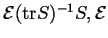 being the expectation operator. A lemma of the
matrix Hessian
being the expectation operator. A lemma of the
matrix Hessian
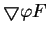 , where
, where
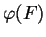 is a scalar
(matrix) function of
is a scalar
(matrix) function of 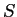 will be proved. Further a lemma on the scalar
Hessian tr
will be proved. Further a lemma on the scalar
Hessian tr
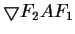 , where
, where 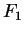 and
and 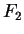 are matrix
functions of
are matrix
functions of
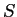 and
and 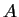 is a constant matrix, will be given. References: Hass, L.
R. (1981) Canadian J. Statist, 215-224. Leung, P. L. (1994) J. Multivariate
Anal. 48, 107-14.
is a constant matrix, will be given. References: Hass, L.
R. (1981) Canadian J. Statist, 215-224. Leung, P. L. (1994) J. Multivariate
Anal. 48, 107-14.



Next: About this document ...
Tohru Okuzono
2001-07-12
![]() . The habitual unbiased estimator of
. The habitual unbiased estimator of
![]() is
is ![]() . Under certain conditions
. Under certain conditions
![]() is better than
is better than ![]() , for suitable
, for suitable
![]() . Leung (1994) showed this using the loss function
. Leung (1994) showed this using the loss function